第1章 实数系和复数系

引言

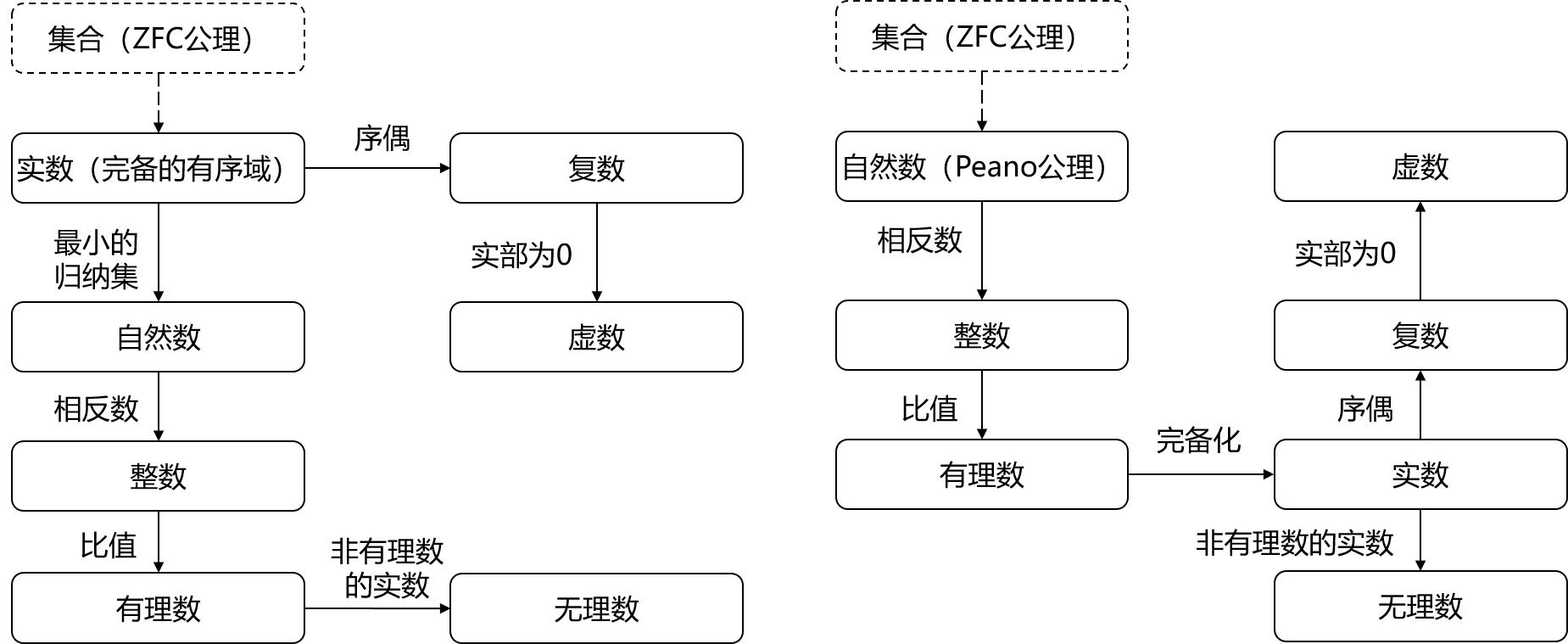
这本书中，作者以公理系统建立实数模型为基础，依次来定义其它自然数、整数、有理数、无理数，最后拓展为复数。逻辑顺序如下面左图所示。此外，也有其它书籍采用右图的逻辑顺序，即以自然数模型为基础，比较符合历史发展。 数系

实数模型依赖10条公理，可以分为三组：域公理，序公理和完全公理（又称上确界公理或连续性公理）。

实数

域公理

公理1 交换律。$x+y=y+x$，$x\cdot y=y\cdot x$。

公理2 结合律。$x+(y+z)=(x+y)+z$，$x\cdot (y\cdot z)=(x\cdot y)\cdot z$。

公理3 分配律。$x\cdot (y+z)=x\cdot y+x\cdot z$。

公理4 对任意$x$，$y$，存在$z$使得$x+z=y$。这个$z$可以用$y-x$表示。而$x-x$用$0$表示。（可以证明$0$不依赖$x$）我们把$0-x$写成$-x$，称为$x$的相反数。

公理5 至少存在一个实数$x\neq 0$。如果$x,y$是两个实数，且$x\neq 0$，则存在实数$z$使得$x\cdot z=y$，这个$z$用$y/x$来表示；数$x/x$用$1$来表示，而且可以证明1不依赖$x$。如果$x\neq 0$，则把$1/x$记为$x^{-1}$，并称为$x$的倒数。

实数域

$(R,+,\cdot)$构成域（field）$\implies (R,+,\cdot)$构成可交换除环。

  1. $(R,\cdot)$可交换$\implies \forall x,y\in R, x\cdot y=y\cdot x$
  2. $(R,+,\cdot)$构成除环（division ring），也称反对称域（skew field）。

$(R,+,\cdot)$构成除环（division ring）

  1. $(R\setminus \{0\},\cdot)$构成群（group）。
  2. $(R,+,\cdot)$构成么环（unitary ring）。

$(R\setminus \{0\},\cdot)$构成群（group）。

  1. 逆元。$\forall x\in R\setminus \{0\}, \exists y\in\setminus \{0\},  x\cdot y=y\cdot x=1$（倒数）
  2. $(R\setminus \{0\},\cdot)$构成半群（semigroup）。（略）

$(R,+,\cdot)$构成么环（unitary ring）。

  1. $(R,\cdot)$构成么半群（monoid）。
  2. $(R,+)$构成阿贝尔群（abelian group），也称交换群（commutative group）。
  3. 分配律。$(x+y)\cdot z=x\cdot z+y\cdot z, x\cdot (y+z)=x\cdot y+ x\cdot z$

$(R,\cdot)$构成么半群（monoid）。

  1. 么元。$\forall x\in R, 1\cdot x=x \cdot 1 =x$
  2. $(R,\cdot)$构成半群（semigroup）。
  • 结合律。$\forall x,y,z\in R, x\cdot (y\cdot z)=(x \cdot y)\cdot z $
  • $(R,\cdot)$构成原群（magma）。
    • 封闭性。$\forall x,y\in R, x\cdot y \in R $

$(R,+)$构成阿贝尔群（abelian group）

  1. 交换律。$\forall x,y\in R,  x+y=y+x $
  2. $(R,+)$构成群（group）。

$(R,+)$构成群（group）。

  1. 逆元。$\forall x\in R, \exists y\in R,  x+y=y+x=0$（相反数）
  2. $(R,+)$构成半群（semigroup）。
  • 结合律。$\forall x,y,z\in R, x+(y+ z)=(x+ y)+ z $
  • $(R,+)$构成原群（magma）。
    • 封闭性。$\forall x,y\in R, x+ y \in R $

序公理

公理6 关系$x<y$、$x>y$和$x=y$中恰有一个成立。

公理7 如果$x<y$，则对任意$z$有$x+z<y+z$。

公理8 如果$x>0$且$y>0$，则$xy>0$。

公理9 如果$x>y$且$y>z$，则$x>z$。

实数是有序域

$(R,+,\cdot)$是有序域（ordered field）。

  1. $(R,+,\cdot)$构成域（field）。见前文。
  2. $\leq$是$R$上的全序（total order）。（全序是任意元素”互相可比较的“，即具有完全性的偏序）

$\leq$是$R$上的全序（total order）

  1. 完全性。$\forall a,b\in R$, 必有$a\leq b$或$b\leq a$
  2. $\leq$是$R$上的偏序（partial order）。
    • 反对称性。$a\leq b，b\leq a \implies a=b$（定义$=$）
    • 传递性。$a\leq b，b\leq c \implies a\leq c$
    • 自反性。$\forall a\in R, a\leq a$（完全性蕴含自反性）
  3. $a\leq b \implies a+c\leq b+c$和$0\leq a, 0\leq b \implies 0\leq a\cdot b$。

（导出）对应全序$\leq$，存在$<$为严格全序（strict total order）。$a<b \iff \neg(b\leq a)$（定义逆补关系$<$）

  1. 弱序性。$<$是严格弱序（strict weak order）。”不可比较的“关系即定义为相等，$a=b \iff \neg(a<b)\land \neg(b<a)$
    • $<$是严格偏序（strict partial order）。
      • 非自反性。不存在$a<a$。
      • 传递性。$a< b，b< c \implies a< c$
      • 非对称性。$a<b\implies \neg(b<a)$（由非自反性和传递性可证）
  2. “不可比较的“关系$\neg(a<b)\land \neg(b<a)$具有传递性。
  3. 三分性。$a<b$、$a=b$和$a<b$有且只有一个成立。

定理1.1：如果$a,b\in R$，对任意的$\varepsilon>0$有$a\leq b+\varepsilon$，则$a\leq b$。

证明：反证法。假设$b<a$。取$\varepsilon=\dfrac{a-b}{2}$，则$b+\varepsilon=b+\dfrac{a-b}{2}=\dfrac{a+b}{2}<\dfrac{a+a}{2}=a$。这与条件$a\leq b+\varepsilon$矛盾，故假设不成立。因此，$a\leq b$。

公理10即完全公理。 见后文。

实数的几何表示

实数解释为直线上的点。在欧几里德几何公理体系下，实数和点一一对应。

数轴：原点（0），单位长度（1），正方向（次序关系）。

区间

定义1.2 假定$a<b$，

  • 开区间$(a,b)=\{x | a<x<b\}$；
  • 闭区间$[a,b]=\{x | a\leq x\leq b\}$

半开区间：

  • 左闭右开区间$[a,b)=\{x | a\leq x<b\}$；
  • 左开右闭区间$(a,b]=\{x | a< x\leq b\}$

无穷区间：

  • $(-\infty,a)=\{x| x<a\}$，
  • $(-\infty,a]=\{x| x\leq a\}$，
  • $(a,+\infty)=\{x| x>a\}$，
  • $[a,+\infty)=\{x| x\geq a\}$

实数集$R$有时被记作$(-\infty, +\infty)$。

单独的一个数有时被认为是退化的闭区间。

注意：$+\infty$和$-\infty$不是实数。只是一种表记方式。所有的实数都是“有限的”。（数是一个固定的值，不能在数轴上移动，想要多大就有多大）

从实数到整数

整数

定义1.3：一个实数集$S$为归纳集，如果

  • $1\in S$
  • $\forall x\in S, 1+x\in S$

例：$R$是归纳集，$R^+$也是归纳集

定义1.4：一个实数是正整数，如果它属于每一个归纳集。正整数集用$Z^+$表示。

性质：$Z^+$是最小的归纳集。归纳法原则。（数学归纳法的基础）

正整数的相反数是负整数。正整数、负整数和$0$，构成整数集，记为$Z$。

整数的唯一因数分解定理

若$n,d\in Z$，存在$c\in Z$使得$n=cd$，则$d$是$n$的一个因数，$n$是$d$的一个倍数，记为$d|n$。

正整数$n>1$。如果正因数只有$1$和$n$，则$n$为素数。否则，$n$为合数。$1$既不是素数，也不是合数。

定理1.5：对于整数$n>1$，或者是一个素数，或者是一些素数的乘积。

证明：归纳法。

i)起始步。$n=2$时，$2$为素数，显然成立。

ii)归纳步。设对$n=2,\cdots,k$均成立。若$k+1$为素数，则显然成立。若$k+1$为合数，则存在正因子$2\geq c,d \leq k$使得$k+1=cd$。因为根据假设，$c,d$为素数或素数的乘积，所以$k+1$也为素数或素数的乘积。

综上，对任意整数$n>1$，$n$为素数或素数的乘积。

若$d|a$且$d|b$，则$d$为$a,b$的公因数。

定理1.6：对于每一对整数$a,b$都存在公因数$d$，形如$$d=ax+by，$$其中$x$和$y$都是整数。而且，$a$和$b$的每一个公因数都能整除这个$d$。

证明：（1）假定$a\geq b\geq 0$。将整数对$a,b$按和进行分类。

命题$P(n)$：对任意的$a+b=n$，①$a,b$存在公因数$d=ax+by$，而且，②$a,b$的每一个公因数都能整除$d$。

然后对$P(n)$使用归纳法证明。

i) 起始步：当$n=0$，则$a=b=0$。取$d=0,x=y=0$，显然$P(n)$成立。

ii) 归纳步：假设当$n=1,2,\cdots,k$均有$P(n)$成立。试证$P(k+1)$成立。

若$b=0$，则取$d=a, x=1, y=0$。显然$P(k+1)$成立。

若$b\geq 1$，则令$a_1=a-b, b_1=b$，其和$n_1=a_1+b_1=a\leq k$。根据假设$P(n_1)$成立。所以$a_1，b_1$有公因数$d=a_1x+b_1y$，且$a_1,b_1$的每一个公因数都能整除$d$。因为$d|a_1+b_1，d|b_1$，所以$d|a,d|b$，即$d$为$a,b$的公因数。同时有$d=(a-b)x+by=ax+b(y-x)$成立（①得证）。此外，$a,b$的每一个公因数都能整除$a$和$b$，那么也就能整除它们的线性组合$d=ax+b(y-x)$（②得证）。因此，$P(k+1)$成立。

综上，对所有的整数$n>1$，命题$P(n)$成立。

(2)若$a, b$中存在负数，则对绝对值$|a|, |b|$应用(1)的证明。

综上，对任意的$a,b$，定理成立。

如果$d$是$a,b$的公因数，且$d=ax+by$，则$-d$是同样形式的公因数：$-d=a(-x)+b(-y)$。这两个公因数中，非负的一个称为$a,b$的最大公因数，记为$\operatorname{gcd}(a,b)$，简记$(a,b)$。如果$(a,b)=1$，则称$a,b$为互素。

定理1.7（欧几里德引理）：若$a|bc$且$(a,b)=1$，则$a|c$。

证明：因为$(a,b)=1$，所以$1=ax+by$。于是，$c=acx+bcy$。因为$a|acx, a|bcy$，所以$a|c$。

定理1.8：如果素数$p$整除$ab$，则$p|a$或$p|b$。更一般地，若$p$整除$a_1\cdots a_k$，则$p$至少整除这些数中的一个。

证明：不妨设$p\not |a$。令$d=(p,a)$，则$d|p$，所以$d=1$或$d=p$。但是$d=p$则$p|a$，因此$d\neq p$。于是$d=1$。若$(p,a)=1$，则$p|b$。

对于多个因子乘积的形式，用归纳法。

i) 起始步。当$k=2$，根据上面的证明，显然成立。

ii) 假设$k$个因子时成立。

若$p|a_1\cdots a_k$，则显然成立。

若$p\not | a_1\cdots a_k$且$p | a_1\cdots a_ka_{k+1}$，设$d=(p,a_1\cdots a_k)$，则$d|p$。所以$d=1$或$d=p$。但是$d=p$则$p| a_1\cdots a_k$，矛盾，因此$d\neq p$。则$d=1$。所以$p|a_{k+1}$。因此，对于k+1个因子，结论也成立。

综上，对于任意多个因子，定理成立。

定理1.9（唯一因数分解定理）：每一个整数$n>1$都可以用唯一的方法表示为素因数之积，不同之处至多是因数的次序。

证明：归纳法。

i) 起始步。$n=2$，本身为素数，显然成立。

ii) 归纳步。设$n=2,\cdots,k$时均成立。

若$n=k+1$为素数，则显然成立。

若$n=k+1$为和数，则设$n$有两种分解方法，比如$$n=p_1p_2\cdots p_s=q_1q_2\cdots q_t。$$根据等式，既然$p_1|q_1q_2\cdots q_t$，则$p_1$整除其中某个因子。重新排列$q_1q_2\cdots q_t$的顺序，使得$p_1|q_1$。因为两者都是素数，所以$p_1=q_1$。因此，等式约去该因子。$$\dfrac{n}{p_1}=p_2\cdots p_s=q_2\cdots q_t$$此时，$1<\dfrac{n}{p_1}\leq k$，根据假设，$\dfrac{n}{p_1}$的这两个因式分解是相同的，不同之处最多只有因数的次序。所以，$n=k+1$时成立。

综上，对于所有的整数$n>1$，定理成立。

这个定理也叫算术基本定理。

从整数到有理数和无理数

有理数

整数的商$\dfrac{a}{b}$（其中$b\neq 0$）称为有理数。

有理数的集合记为$Q$。

性质：$Q$满足所有的域公理和序公理。$\implies (Q,+,\cdot)$是有序域。

无理数

非有理数的实数称为无理数。

定理1.10：$n$是一个正整数，却不是一个完全平方数，则$\sqrt{n}$是无理数。

证明：（1）$n$不含有大于$1$的平方因数。

假设$\sqrt{n}$是有理数。设$\sqrt{n}=\dfrac{a}{b}$，其中$a$和$b$互素。则$n^2b=a^2$。左边是$n$的倍数，则右边$a^2$必然也是$n$的倍数。因为$n$没有大于$1$的平方因数，所以$a$是$n$的倍数。于是$a=cn$，其中$c$是某个整数。所以$nb^2=c^2n^2$，即$b=c^2n$。同理可证，$b$也是$n$的一个倍数。这与$a,b$互素的假设矛盾。因此，$\sqrt{n}$不是有理数。

（2）$n$含有大于$1$的平方因数。

设$n=m^2k$，其中$k>1$没有大于$1$的平方因数。于是$\sqrt{n}=m\sqrt{k}$。若$\sqrt{n}$是有理数，则$\sqrt{k}$也是有理数。这与(1)的结论矛盾。因此，$\sqrt{n}$不是有理数。

综上，$\sqrt{n}$不是有理数。定理得证。

定理1.11：若$e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots+\dfrac{x^n}{n!}+\cdots$，则$e$是无理数。

证明：先证$e^{-1}$是无理数。因为$e^{-1}$是交错级数，每一项绝对值在减小，所以截断后的误差是与忽略掉的第一项同号，绝对值小于该项的绝对值。因此，设$S_n=\sum_{k=0}^{n}\dfrac{(-1)^k}{k!} $，则$$0<e^{-1}-S_{2k-1}<\frac{1}{2k!}$$对于任意的整数$k>1$，$$0<(2k-1)!(e^{-1}-S_{2k-1})<\frac{1}{2k}\leq \frac{1}{2}。$$显然$(2k-1)!S_{2k-1}$是整数。若$e^{-1}$是有理数，则设$e^{-1}=a/b$。而当$k\geq b$时，$(2k-1)!e^{-1}$也是整数。两个整数的差在$0$和$\dfrac{1}{2}$之间，这是不可能的。因此，$e^{-1}$是不是有理数。所以，$e$是无理数。

实数的完备性

上界，最大元，最小上界（上确界）

有理数$Q$是满足九条公理的，即$(Q,+,\cdot)$是有序域。但是在这九条公理下，方程$x^2=0$无解。因此，需要增加一个完全公理，来包含无理数。所以，实数系有十条公理。

定义1.12：设$S$是一个由实数组成的集合。如果有一个实数$b$对于$S$中的每一个$x$都有$x\leq b$，则称$b$是$S$的一个上界，并说$S$以$b$为上界。

如果$b$是$S$的一个元素，则称$b$是$S$的最大元或最大元素。如果这样的$b$存在，则是唯一的，记为$b=\max S$。

没有上界的集合称为上无界的。

类似地，可以定义下界>，下有界，最小元素（或最小元）。如果$S$存在最小元，则记为$\min S$。

某些集合是有上界的，但却没有最大元。因此需要一个概念来代替最大元，称为最小上界或上确界。

定义1.13：设设$S$是一个有上界的实数集合。实数$b$称为$S$的上确界，如果它具有如下两条性质：

  1. $b$是$S$的一个上界，
  2. 小于$b$的数都不是$S$的上界

一个集合不能有两个不同的最小上界，因此上确界是唯一的，记为$b=\operatorname{sup} S$。如果$S$有最大元，则$\max S=\operatorname{sup} S$。

类似地，可以定义$S$的最大下界或下确界，用$\operatorname{inf} S$表示。

完全公理

公理10：每一个上有界的非空实数集$S$都有上确界；也就是说，有一个实数$b$使得$b=\operatorname{sup} S$。

推论：每一个下有界的非空实数集$S$都有下确界；也就是说，有一个实数$b$使得$b=\operatorname{inf} S$。

上确界的某些性质

定理1.14（逼近性质）：设$S$是一个有上确界的非空实数集，记$b=\sup S$。则对于每一个$a<b$，在$S$中都有某个$x$使得$$a<x\leq b。$$

证明：首先，对于$S$中的一切$x$都有$x\leq b$。如果对于$S$中的一切$x$都有$x\leq a$，则$a$是一个比最小上界还小的上界。这与最小上界的定义矛盾。所以$S$中至少有一个$x$使$x>a$。

定理1.15（可加性质）：给定$R$的非空子集$A$与$B$，设$C$表示集合$$C=\{x+y|x\in A, y\in B\}。$$如果$A$和$B$都有上确界，则$C$也有上确界，且有$$\sup C=\sup A+\sup B。$$

证明：假设$a=\sup A, b=\sup B$。若$z\in C$，则有$z=x+y$，其中$x\in A, y\in B$。所以$z=x+y\leq a+b$。于是，$a+b$是$C$的一个上界。所以根据公理10，$C$有上确界，记$c=\sup C$。则由上确界定义，$c\leq a+b$。

任取$\varepsilon >0 $，由定理1.14，在$A$中有$x$，$B$中有$y$使得$$a-\varepsilon<x, b-\varepsilon<y。$$两式相加得$$a+b-2\varepsilon<x+y。$$于是，对于每个$\varepsilon >0 $都有$a+b<x+y+2\varepsilon$。由定理1.1知，$a+b\leq c$。

综上，$a+b=c$，即$\sup C=\sup A+\sup B$，证毕。

定理1.16（比较性质）给定$R$的非空子集$S$和$T$使得对于$S$中的每一个$s$和$T$中的每一个$t$都有$s\leq t$。那么，如果$T$有上确界，则$S$有上确界，且有$$\sup S\leq \sup T。$$

证明：设$t_0=\sup T$。根据对任意$t\in T$，有$t\leq t_0$。又因为对于任意$s\in S$都有$s\leq t$。所以$t_0$是$S$的一个上界。因此$S$有上确界。设$s_0=\sup S$。若$s_0>t_0$，则$t_0$是比$s_0$更小的$S$的上界。这与上确界定义矛盾。因此$\sup S\leq \sup T$。证毕。

从完全公理推演出的整数性质

定理1.17 由正整数$1,2,3,\cdots$组成的集合$Z^+$是上无界的。

证明： 如果$Z^+$是上有界的，则$Z^+$将有上确界，记$a=\sup Z^+$。按照定理1.14，对$Z^+$中的某个$n$有$a-1<n\leq a$。于是对于这个$n$有$n+1>n$，而$n+1\in Z^+$，这个同$a=\sup Z^+$矛盾。

定理1.18 对于每一个实数$x$都有正整数$n$使得$n>x$。

证明：如果不存在$n>x$，则对任意$n$有$n\leq x$成立，于是$x$为$Z^+$的一个上界。这与定理1.17矛盾。

实数系的阿基米德性质

任何线段不论多长，它都可以被有限条有一个给定长度的线段覆盖，而且不论这个给定的正长度有多小。

定理1.19 如果$x>0$而$y$是任意一个实数，则存在一个正整数$n$使得$nx>y$。

证明：在定理1.18中，将$\dfrac{y}{x}$代替$x$。

实数的小数表示

能用有限小数表示的有理数

形如$$r=a_0+\dfrac{a_1}{10}+\dfrac{a_2}{10^2}+\cdots +\dfrac{a_n}{10^n}$$的实数，其中$a_0$是非负整数，$a_1,a_2,\cdots,a_n$是满足$0\leq a_i \leq 9$的整数，通常更简明地写为$$r=a_0.a_1a_2\cdots a_n。$$这种记法称为$r$的有限小数表示。

这种实数都是有理数。它们都有形如$r=\dfrac{a}{10^n}$这种形式，其中$a$是一个整数。

不是一切有理数都能用有限小数表示，比如$\dfrac{1}{3}$。如果能表示，则存在某个$a$使得$\dfrac{1}{3}=\dfrac{a}{10^n}$或$3a=10^n$。这是不可能的，3不能整除10的任何次幂。

用有限小数逼近实数

定理1.20 设$x\geq 0$，则对于任何整数$n\geq 1$存在有限小数$r_n=a_0.a_1a_2\cdots a_n$使得$$r_n\leq x <r_n+\dfrac{1}{10^n}。$$

证明：设$S$是所有$\leq x$非负整数构成的集，因为$0\in S$，则$S$非空，而且$S$以$x$为上界。所以$S$有上确界，记$a_0=\sup S$。$a_0\in S$。所以$a_0$是一个非负整数。我们称$a_0$为$x$中的最大整数，记为$a_0=[x]$。显然有 $$a_0\leq x <a_0+1。$$ 设$a_1=[10x-10a_0]$，它是不超过$10x-10a_0$的最大整数。因为$0\leq 10x-10a_0=10(x-a_0)<10$，所以有$0\leq a_1 \leq 9$，而且 $$a_1\leq 10x-10a_0 <a_1+1。$$ 因此，$a_1$是满足不等式 $$a_0+\frac{a_1}{10}\leq x <a_0+\frac{a_1+1}{10}$$ 的最大整数。

更一般地，在选取$a_1,\cdots,a_n$满足$0\leq a_i \leq 9$之后，设$a_n$满足不等式 $$a_0+\frac{a_1}{10}+\cdots + \frac{a_n}{10^n} \leq x <a_0+\frac{a_1}{10}+\cdots + \frac{a_n+1}{10^n}$$ 的最大整数，则$0\leq a_n \leq 9$，且有 $$r_n \leq x <r_n + \frac{1}{10^n}，$$ 其中$r_n =a_0.a_1a_2\cdots a_n$。$x$实际是有理数$r_1,r_2,\cdots$构成的集合的上确界。

用无限小数表示实数

在定理1.20的证明中，对于给定$x$，整数$a_0,a_1,a_2,\cdots $可以无限求下去。定义为$x$的无限小数表示。

如果使用下式 $$a_0+\frac{a_1}{10}+\cdots + \frac{a_n}{10^n} < x \leq a_0+\frac{a_1}{10}+\cdots + \frac{a_n+1}{10^n}$$ 则会得到稍微不同的小数展开式的定义。此时有限小数$r_n$满足条件$r_n<x\leq r_n+10^{-n}$。

一个实数可以有两种不同的小数表示式。$\implies$两个不同的实数集可以有相同的上确界。

实数的重要不等式

绝对值与三角不等式

如果$x$是任一实数，则$x$的绝对值（记为$|x|$）定义为：$$\displaystyle{|x| = \left\{\begin{array}{ll} x, & x\geq 0,\ -x, & x<0。\end{array} \right. } $$

定理1.21 若$a>0$，则$|x|\leq a$当且仅当$-a\leq x\leq a$。

证明：根据定义$|x|=x$或$|x|=-x$，可得不等式$-|x|\leq x \leq |x|$。又有$|x|\leq a$，所以$-a\leq -|x|\leq x \leq |x| \leq a$。反过来，已知$-a\leq x \leq a$。则当$x\geq 0$时，$|x|=x\leq a$；当$x<0$时，$|x|=-x \leq a$。因此$|x|\leq a$。

定理 1.22 （三角不等式）对任意实数$x$和$y$都有$$|x+y|\leq |x|+|y|。$$

证明：由$-|x|\leq x \leq |x|$和$-|y|\leq y \leq |y|$相加可得$-(|x|+|y|)\leq x+y \leq |x|+|y|$。由定理1.21，$|x+y|\leq |x|+|y|$。

三角不等式的其它形式。例如：在定理1.22中令$x=a-c,y=c-b$可得$$|a-b|\leq |a-c|+|c-b|。$$定理1.22移项可得$|x|\geq |x+y|-|y|$，再令$x=a+b,y=-b$可得$$|a+b|\geq |a|-|b|。$$交换$a$，$b$位置得$|a+b|\geq |b|-|a|=-(|a|-|b|)$，于是$$|a+b|\geq ||a|-|b||。$$

用归纳法还可以证明三角不等式的推广$$|x_1+x_2+\cdots +x_n|\leq |x_1|+|x_2|+\cdots +|x_n|$$和$$|x_1+x_2+\cdots +x_n|\geq |x_1|-|x_2|-\cdots -|x_n|。$$

柯西-施瓦茨不等式

定理1.23 （柯西-施瓦茨不等式）若$a_1,\cdots , a_n$和$b_1,\cdots ,b_n$是任意实数，则有$$\left(\sum_{k=1}^n a_kb_k\right)^2\leq\left(\sum_{k=1}^n a_k^2\right)\left(\sum_{k=1}^n b_k^2\right)。$$此外，如果有某个$a_i\neq 0$，则上式等号当且仅当存在一个实数$x$使得对于每一个$k=1,2,\cdots ,n$都有$a_kx+b_k=0$时成立。

证明：平方和永远非负，因此对每一个实数$x$都有$$\sum_{k=1}^n (a_kx+b)^2\geq 0。$$其中等号当且仅当每一项都等于$0$时成立。和的平方可以展开，变为$$Ax^2+2Bx+C\geq 0，$$其中$$A=\sum_{k=1}^na_k^2，B=\sum_{k=1}^n a_kb_k，C=\sum_{k=1}^nb_k^2。$$如果$A>0$，令$x=-B/A$可得$B^2-AC\leq 0$，即要证的不等式。如果$A=0$，则$a_i$均为$0$，从而$B=0$。于是$C\geq 0$成立。

正负无穷和扩充实数系$R^*$

定义1.24 所谓扩充的实数系$R^*$是指实数集$R$加上$+\infty$和$-\infty$这两个符号，它们满足下述性质：

  1. 若$x\in R$，则有$$\begin{array}{ll}x+(+\infty)=+\infty，& x+(-\infty)=-\infty \\ x-(+\infty)=-\infty，& x-(-\infty)=+\infty \\ x/(+\infty)=x/(-\infty)=0。& \end{array}$$
  2. 若$x>0$，则有$$x(+\infty)=+\infty，x(-\infty)=-\infty。$$
  3. 若$x<0$，则有$$x(+\infty)=-\infty，x(-\infty)=+\infty。$$
  4. 无穷的四则运算$$\begin{array}{l}(+\infty)+(+\infty)=(+\infty)(+\infty)=(-\infty)(-\infty)=+\infty，\\ (-\infty)+(-\infty)=(+\infty)(-\infty)=-\infty 。\end{array}$$
  5. 如果$x\in R$，则有$-\infty <x <+\infty$。

记号 $(-\infty ,+\infty)$表示$R$，$[-\infty ,+\infty]$表示$R^*$。$R$中的点称为“有限的”，以区别于“无限的”点$+\infty$和$-\infty$。

定义 1.25 每一个开区间$(a,+\infty)$称为$+\infty$的一个邻域，或称为以$+\infty$为中心的一个球。每一个开区间$(-\infty, a)$称为$-\infty$的一个邻域，或称为以$-\infty$为中心的一个球。

从实数到复数

复数

从序公理可知，实数的平方是非负的。像$x^2=-1$这样的方程在实数范围内无解。于是，需要引入复数，使得形如$$a_0+a_1x+\cdots +a_nx^n=0$$的一般代数方程在复数范围内都有解，其中系数$a_0,a_1,\cdots,a_n$是任意实数。（这称为代数基本定理）

定义 1.26 一个复数是用$(x_1,x_2)$表示一个有序实数对。第一个数$x_1$称为这个复数的实部，第二个数$x_2$称为这个复数的虚部。两个复数$x=(x_1,x_1)$和$y=(y_1,y_2)$称为相等（记为$x=y$）当且仅当$x_1=y_1$，$x_2=y_2$。它们的和$x+y$及乘积$xy$分别用等式$$x+y=(x_1+y_1,x_2+y_2)，xy=(x_1x_2-y_1y_2, x_1y_2+x_2y_1)$$来定义。

全体复数的集合用$C$来表示。

定理 1.27 复数的加法和乘法运算满足交换律，结合律和分配律。

定理 1.28

  • 加法的幺元：$(x_1,x_2)+(0,0)=(x_1,x_2)$；加法的逆元：$(x_1,x_2)+(-x_1, -x_2)=(0,0)$。
  • 乘法的零元：$(x_1,x_2)(0,0)=(0,0)$；乘法的幺元：$(x_1,x_2)(1,0)=(x_1,x_2)$。

定理 1.29 （减法）给定两个复数$x=(x_1,x_2)$和$y=(y_1,y_2)$，则存在一个复数$z$使得$x+z=y$。事实上，$z=(y_1-x_1, y_2-x_2)$。这个复数$z$用$y-x$来表示。复数$(-x_1,-x_2)$用$-x$来表示。

定理 1.30 对于任何两个复数$x$和$y$都有$$(-x)y=x(-y)=-(xy)=(-1,0)(xy)。$$

定义 1.31 （除法）如果$x=(x_1,x_2)\neq (0,0)$，$y$是复数，则定义$$x^{-1}=\left(\frac{x_1}{x_1^2+x_2^2},\frac{x_2}{x_1^2+x_2^2}\right), \frac{y}{x}=yx^{-1}。$$

定理 1.32 如果$x$与$y$都是复数，$x\neq (0,0)$，则存在一个复数$z$使得$xz=y$，即$z=yx^{-1}$。

定理 1.33 形如$(x,0)$的复数与实数具有同样的算术性质。$$(x_1,0)+(y_1,0)=(x_1+y_1,0)，$$ $$(x_1,0)(y_1,0)=(x_1y_1,0)，$$ $$(x_1,0)/(y_1,0)=(x_1/y_1,0)，(y_1\neq 0)。$$

复数的几何表示

复数可以用平面上的点来表示。加法按平行四边形法则相加。（高斯1799，阿尔冈1806）

从北极把球面上的点投影到南极处的切平面上。除了北极外，球面上的点与平面上的点一一对应。（球极平面投影，黎曼）

虚数单位

定义 1.34 复数(0,1)用$i$表示，称为虚数单位。

定理 1.35 每个复数$x=(x_1,x_2)$都能表示成$x=x_1+ix_2$的形式。

证明：$x_1=(x_1,0)$， $ix_2=(0,1)(x_2,0)=(0,x_2)$，$x_1+ix_2=(x_1,0)+(0,x_2)=(x_1,x_2)$。

定理 1.36 $i^2=-1$。

证明：$i^2=(0,1)(0,1)=(-1,0)=-1$。

复数的绝对值

定义 1.37 如果$x=(x_1,x_2)$，则定义$x$的模或称为绝对值为等式$$|x|=\sqrt{x_1^2+x_2^2}$$的非负实数。

定理 1.38

  1. $|(0,0)|=0$，且当$x\neq 0$时$|x|>0$。
  2. $|xy|=|x||y|$。
  3. $\left|\dfrac{x}{y}\right|=\dfrac{|x|}{|y|}$，当$y \neq 0$。
  4. $|(x_1,0)|=|x_1|$。

证明：(i)和(iv)是明显的。现在证明(ii)。令$x=x_1+ix_2$，$y=y_1+iy_2$，则$xy=x_1y_1-x_2y_2+i(x_1y_2+x_2y_1)$。于是$$|xy|^2=x_1^2y_1^2+x_1^2y_2^2+x_2^2y_1^2+x_2^2y_2^2=(x_1^2+y_1^2)(x_2^2+y_2^2)=|x|^2|y|^2。$$等式(iii)可以在(ii)中$|x|=|y||x/y|$导出。

几何上，$x$表示原点到$x$的距离。$|x-y|$表示$x$到$y$两点间的距离。

定理 1.39 如果$x$和$y$都是复数，则有$$|x+y|\leq |x|+|y|。$$

复数排序的不可能性

因为复数不能像实数那样同时满足序公理6,7,8。

虚数单位$i\neq 0$，由公理6，必有$i>0$或$i<0$。假定$i>0$，由公理8，$i^2=-1>0$。由公理7，两边加$1$得$0>1$。另一方面，$-1>0$由公理8可得$1>0$。这样既$0>1$又$1>0$，由公理6，这是不可能的。因此$i>0$导致矛盾。类似地，$i<0$也会导致矛盾。

复指数

当实数$x$为指数时，$e^x$的性质：$e^{x_1}e^{x_2}=e^{x_1+x_2}$和$e^0=1$。

记$z=x+iy$（$x$，$y$为实数），希望保持性质$e^{x+iy}=e^xe^{iy}$。因此需要定义$e^{iy}$表示什么。

定义 1.40 如果$z=x+iy$，则定义$e^z=e^{i+iy}$为复数$e^z=e^x(\cos y +i\sin y)$。

定理 1.41 如果$z_1=x_1+iy_1$和$z_2=x_2+iy_2$为两个复数，则有$e^{z_1}e^{z_2}=e^{z_1+z_2}$。

证明：由定义$$e^{z_1}=e^{x_1}(\cos {y_1} +i\sin {y_1}), \quad e^{z_2}=e^{x_2}(\cos {y_2} +i\sin {y_2})。$$于是$$e^{z_1}e^{z_2}=e^{x_1}e^{x_2}[\cos y_1 \cos y_2 -\sin y_1 \sin y_2 + i(\cos y_1 \sin y_2 +\sin y_1 \cos y_2)]。$$因为$x_1$和$x_2$为实数，还有三角公式$$\cos y_1 \cos y_2 -\sin y_1 \sin y_2=\cos (y_1+y_2)$$和$$\cos y_1 \sin y_2 +\sin y_1 \cos y_2)=\sin (y_1+y_2)。$$于是可得$$e^{z_1}e^{z_2}=e^{x_1+x_2}[\cos (y_1+y_2)+ i(\sin y_1+y_2)]=e^{z_1+z_2}。$$

复指数的进一步性质

定理 1.42 $e^z$永不为零。

证明：$e^ze^{-z}=e^0=1$，因而$e^z$不能为$0$。

定理 1.43 如果$x$为实数，则$|e^{ix}|=1$。

证明：$|e^{ix}|^2=\cos^2 x+\sin^2 x=1$，且$|e^{ix}|>0$。

定理 1.44 $e^x=1$当且仅当$x$是$2\pi i$的整数倍。

证明：如果$z=2\pi i n$，其中$n$是整数，则有$$e^x=\cos(2\pi n)+i\sin (2\pi n)=1。$$反过来，假设$e^z=1$，则$e^x\cos y=1$和$e^x\sin y=0$。因为$e^x \neq 0$，则$\sin y=0$，所以$y=k\pi$，其中$k$是整数。又$\cos (k\pi)=(-1)^k$，$e^x\cos (k\pi)=1$，所以$e^x=(-1)^k$。因为$e^x>0$，所以$k$必定是偶数。于是$e^x=1$，$x=0$。

定理 1.45 $e^{z_1}=e^{z_2}$当且仅当$z_1-z_2=2\pi in$（其中$n$是一个整数）时成立。

证明：$e^{z_1}=e^{z_2}$当且仅当$e^{z_1-z_2}=1$。

复数的辐角

用极坐标$r$和$\theta$表示点$z=(x,y)=x+iy$。令$x=r\cos\theta$，$y=r\sin\theta$，则$z=r\cos\theta+ir\sin\theta=re^{i\theta}$。$r$和$\theta$可以唯一地确定$z$。反过来，$z$也能确定$r=|z|$，但是不能确定$\theta$。无穷多个$\theta$满足$x=|z|\cos\theta$，$y=|z|\sin\theta$，它们相差$2\pi$的整数倍。每一个都称为辐角，其中一个命名为辐角主值。

定义 1.46 设$z=x+iy$是一个非零复数，满足条件$$x=|z|\cos \theta, y=|z|\sin \theta, -\pi<\theta\leq +\pi$$的唯一的实数$\theta$称为辐角主值，记为$\theta=\arg(z)$。

定理 1.47 每一个复数$z\neq 0$都可以用$z=re^{i\theta}$的形式来表示，其中$r=|z|$，$\theta=\arg{z}+2\pi n$，$n为任意整数$。

注记：这种表示方法在乘法，除法中特别有用，因为$$r_1e^{i\theta_1}r_2e^{i\theta_2}=r_1r_2e^{\theta_1+\theta_2}, \frac{r_1e^{i\theta_1}}{r_2e^{i\theta_2}}=\frac{r_1}{r_2}e^{i(\theta_1-\theta_2)}。$$

定理 1.48 如果$z_1z_2\neq 0$，则有$$\arg(z_1z_2)=\arg(z_1)+\arg(z_2)+2\pi n(z_1,z_2)，$$其中$$n(z_1,z_2)=\begin{cases}0, & -pi<\arg(z_1)+\arg(z_2)\leq +\pi，\ +1, & -2\pi <\arg(z_1)+\arg(z_2) \leq -\pi \ -1， & \pi <\arg(z_1)+\arg(z_2) \leq 2\pi。\end{cases}$$

证明：记$z_1=|z_1|e^{i\theta_1}$，$z_2=|z_2|e^{i\theta_2}$，其中$\theta_1=\arg(z_1)$，$\theta_2=\arg(z_2)$，则$z_1z_2=|z_1z_2|e^{i(\theta_1+\theta_2)}$。由$-\pi<\theta_1\leq +\pi$和$-\pi<\theta_2\leq +pi$可知$-2\pi<\theta_1+\theta_2\leq +2\pi$。因此存在一个整数$n$使得$-\pi<\theta_1+\theta_2+2\pi n\leq +\pi$。这个$n$即定理中给出的$n(z_1,z_2)$，而且$$\arg(z_1,z_2)=\theta_1+\theta_2+2\pi n。$$

复数的整数幂和方根

定义1.49 给定复数$z$和整数$n$，定义$z$的$n$次幂如下：

$z^0=1$，$z^{n+1}=z^nz$，当$n\geq 0$，

$z^{-n}=(z^{-1})^n$，当$z\neq 0$且$n>0$。

定理1.50 给定两个整数$m$和$n$，对于$z\neq 0$有$$z^nz^m=z^{n+m}，(z_1z_2)^n=z_1^nz_2^n。$$

定理1.51 如果$z\neq 0$，$n$是一个正整数，则恰好存在$n$个不同的复数$z_0$，$z_1$，$\cdots$，$z_{n-1}$（称为$z$的$n$次方根），使得对于$k=0,1,2,\cdots ,n-1$中的每一个值都有$$z_k^n=z。$$而且，这些方根由下面公式给出：

$z_k=Re^{i\phi_k}$，其中$R=|z|^{1/n}$，

$\phi_n=\frac{\arg(z)}{n}+\frac{2\pi k}{n} \quad (k=0,1,2,\cdots ,n-1)$。

注：$z$的$n$个方根等距离地分布在以原点为中心，以$R=|z|^{1/n}$为半径的圆周上。

证明：这$n$个复数$Re^{i\phi_k}(0\leq k\leq n-1)$是不同的，而且每一个数都是$z$的$n$次方根，因为$$(Re^{i\phi_k})^n=R^ne^{in\phi_k}=|z|e^{i[\arg(z)+2\pi k]}=2。$$现在证明$z$没有其它$n$次方根。假定$w=Ae^{i\alpha}$是一个复数，使得$w^n=z$，则有$|w|^n=|z|$。于是$A^n=|z|$，$A=|z|^{1/n}$。从而可以把$w^n=z$写为$e^{in\alpha}=e^{i[\arg(z)]}$，这意味着$$n\alpha-\arg(z)=2\pi k，$$ $k$是某个整数。于是$\alpha=[\arg(z)+2\pi k]/n$。当$k$取遍所有整数值时，$w$只能取到$z_0$，$z_1$，$\cdots$，$z_{n-1}$这些不同的值。

复对数

定理 1.52 如果$z$是一个非零复数，则存在复数$w$使得$e^w=z$。一个这样的复数$$\ln |z|+i\arg(z)，$$而其他满足条件的$w$形如$$\ln |z| + i\arg(z) +2\pi n，$$其中$n$是一个整数。

证明：由于$e^{\ln |z|+i\arg(z)}=e^{\ln |z|}e^{i\arg(z)}=|z|e^{i\arg(z)}=z$，所以$w=\ln |z|+i\arg(z)$是方程$e^w=z$的一个解。若存在其它解$w_1$，则$e^w=e^{w_1}$，从而$w-w_1=2n\pi i$。

定义 1.53 设$z\neq 0$是一个给定的复数。如果$w$是一个复数使得$e^w=z$，则称$w$为$z$的一个对数。$z$有一个特殊的对数值由$$w=\log |z| +i \arg(z)$$给出，称为$z$的对数主值，而把这个$w$记为$$w=\operatorname{Log} z。$$

定理 1.54 如果$z_1,z_2\neq 0$，则$$\operatorname{Log}(z_1z_2) = \operatorname{Log}z_1 + \operatorname{Log}z_2 + 2\pi i n(z_1,z_2)，$$其中$n(z_1,z_2)$是定理1.48中定义的那个整数。

证明：$$\begin{array}{rcl}\operatorname{Log}(z_1z_2) &=& \log |z_1z_2| + i\arg(z_1z_2) \\ &=& \log |z_1| +\log |z_2| + i[\arg(z_1)+\arg(z_2)+2\pi n(z_1,z_2)]。\square\end{array}$$

复幂

定义 1.55 如果$z\neq 0$，$w$是任意一个复数，则定义$$z^w=e^{w\operatorname{Log}z}。$$

定理 1.56 $z^{w_1}z^{w_2}=z^{w_1+w_2}$，只要$z\neq 0$。

证明：$z^{w_1+w_2}=e^{(w_1+w_2)\operatorname{Log}z}=e^{w_1\operatorname{Log}z}e^{w_2\operatorname{Log}z}=z^{w_1}z^{w_2}$。

定理 1.57 如果$z_1z_2\neq 0$，则有$$(z_1z_2)^w=z_1^wz_2^we^{2\pi i w n(z_1,z_2)}，$$其中$n(z_1,z_2)$是定理1.48中定义的整数。

证明：$(z_1z_2)^w=e^{w\operatorname{Log}(z_1z_2)}=e^{w[\operatorname{Log}z_1+\operatorname{Log}z_2+2\pi i n(z_1,z_2)]}$。

复正弦和复余弦

定义 1.58 给定一个复数$z$，定义$$\cos z=\dfrac{e^{iz}+e^{-iz}}{2}，\quad \sin z=\dfrac{e^{iz}-e^{-iz}}{2}。$$

注：当$z$为实数，则与定义1.40一致。

定义 1.59 如果$z=x+iy$，则有$$\begin{array}{rcl}\cos z &=& \cos x \cosh y -i\sin x \sinh y，\\ \sin z &=& \sin x\cosh y + i\cos x \sinh y。\end{array}$$

证明：$$\begin{array}{rcl}2\cos z &=& e^{iz}+e^{-iz}=e^{-y}(\cos x+i\sin x)+e^y(\cos x+ i\sin x) \\ &=& \cos x(e^y+e^{-y}) -i\sin x(e^y-e^{-y})=2\cos x \cosh y -2i\sin x \sinh y。\end{array}$$对于$\sin z$也可类似证明。

无穷远点与扩充复平面$C^*$

加入一个想象中的点，用符号$\infty$表示。

定义 1.60 所谓扩充复平面$C^*$，指的是除了复平面$C$以外，再添加一个满足下列性质的符号$\infty$：

  1. 如果$z\in C$，则有$z+\infty=z-\infty=\infty$，$z/\infty=0$。
  2. 如果$z\in C$但$z\neq 0$，则$z\cdot \infty=\infty$，$z/0=\infty$。
  3. $\infty+\infty=\infty \cdot \infty= \infty$。

定义 1.61 $C$中的每一个形如$\left\{ z| |z|>r\geq 0\right\}$的集合都叫作$\infty$的一个邻域，或叫作一个以$\infty$为中心的球。

实数$R$因为有序关系$<$，所以需要两个符号$+\infty$和$-\infty$，而复数$C$则只需要一个符号$\infty$即可。

考虑球极平面投影，整个球面上来看，北极点是例外的。其它所有的点都能投影到复平面，与复数$C$一一对应。但是北极点不行。可以把北极点视为$\infty$，于是整个球面上的点与$C^*$可以一一对应。复平面上一个“大“圆的外部的点，根据投影关系，对应于北极附近的”小“球冠。因此用$|z|>r$来定义$\infty$的邻域。